This airborne campaign has two main goals:
1 – Measure atmospheric phenomena for “island wake” detection (air and ocean phenomena).
In geophysics, “island wakes” is a term typically used to refer to atmospheric circulations induced by mountainous islands (atmospheric wakes) as well as ocean effects induced by the islands bathymetry (ocean wakes). In turn, ocean wakes, can be grouped into two main categories (i) wakes induced by atmospheric phenomena (wind wakes), and (ii) wakes induced by oceanic phenomena. Both Atmospheric and oceanic wakes have been subject of many studies by the scientific community.
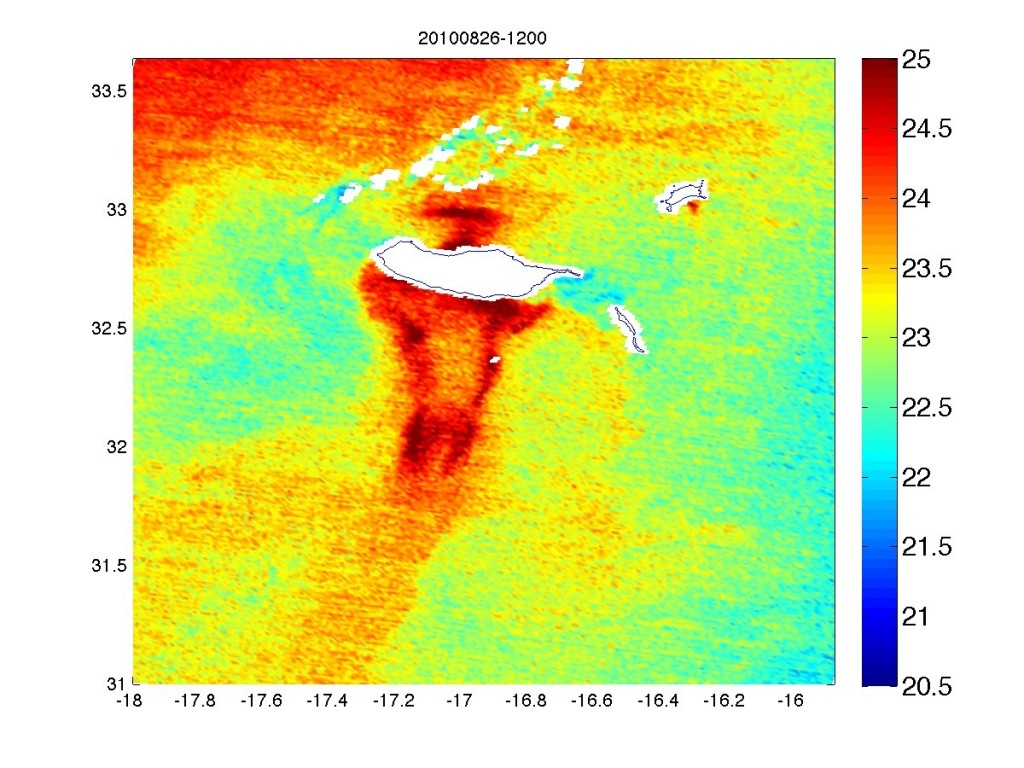
In the next picture you can find an SST graph (Sea Surface Temperature)
This result is for day 26 Ago. and has been taken from MODIS Satellite.
2 – Gravimetry measures for Madeira geoid construction.
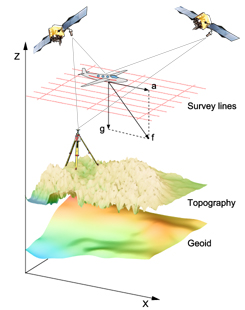
Airborne gravimetry is one of the most important techniques for providing gravity data in areas that are not covered by ongoing and future satellite missions, in an efficient manner. Due to advancements in methodology and system design, the spatial resolution of the Earth’s gravity field has been increased to less than 5 km with high accuracy. The pre-processing of airborne gravity measurements usually results in a set of gravity disturbances at flight level. For the inversion of these observations into gravity functionals at geoid level, a new approach that combines several pre-processing steps, such as filtering, gridding and adjustment of cross-over misfits, with the parameter estimation is being developed. The approach is based on a spectral representation of the gravity field. The gravitational potential is parameterized as a linear combination of harmonic functions, which are fundamental solutions of Laplace’s equation in Cartesian coordinates. The parameters of this representation are estimated using least-squares techniques. An important aspect of the developed technique is that a frequency dependent weighting to handle colored observation noise is applied instead of the traditional low-pass filtering.

We will use the Least-Squares Collocation technique to compute the geoid out of the observed gravity disturbances. The method of Bas Alberts, which is explained in your text, has some drawbacks when the flight paths are not very dense.